Adapted by Nelson Nuñez-Rodriguez
Conditions of Use:

Unless otherwise noted, this work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
Chapters derived from:
By David W. Ball
 Attribution-NonCommercial-ShareAlike
Attribution-NonCommercial-ShareAlike
CC BY-NC-SA
Click on the printer icon at the bottom of the screen
![]()
Make sure that your printout includes all content from the page. If it doesn't, try opening this guide in a different browser and printing from there (sometimes Internet Explorer works better, sometimes Chrome, sometimes Firefox, etc.).
If the above process produces printouts with errors or overlapping text or images, try this method:
Opening EssayMore than 70% of the earth’s surface is covered by a very important solution—seawater. It is likely that without seawater, no life would exist on Earth. At its simplest, seawater is mostly H2O. But about 3.5% of seawater is dissolved solids, mostly NaCl but other ions as well. Table 10.1 "Percentage by Mass of Ions in Seawater and Blood" lists the percentage by mass of the various ions in seawater. Because it is highly likely that life on Earth originated in the oceans, it should not be surprising that many bodily fluids resemble seawater—especially blood. Table 10.1 "Percentage by Mass of Ions in Seawater and Blood" also lists the percentage by mass of ions in a typical sample of blood. Table 10.1 Percentage by Mass of Ions in Seawater and Blood
Most ions are more abundant in seawater than they are in blood, with some notable exceptions. There is far more hydrogen carbonate ion (HCO3−) in blood than in seawater; indeed, it is the third most common ion in blood. This difference is significant because the HCO3− ion and some related species [CO32−, CO2(aq)] have an important role in controlling the acid-base properties of blood. Although there is a negligible amount of the two hydrogen phosphate ions (HPO42− and H2PO4−) in seawater, there is a small amount in blood, where these ions affect acid-base properties. Another notable difference is that blood has a negligible amount of the sulfate ion (SO42−), but this ion is present in seawater. Gold is present in seawater—but only a tiny amount. A current estimate of the amount of gold is about 1 part per every 1 × 1013 parts of seawater, which makes the extraction of gold from seawater unfeasible. However, it does mean that there are about 1.4 × 1014 g of gold in the world’s oceans! |
A solution is a homogeneous mixture—a mixture of two or more substances that are so intimately mixed that the mixture behaves in many ways like a single substance. Many chemical reactions occur when the reactants are dissolved in solution. In this chapter, we will introduce concepts that are applicable to solutions and the chemical reactions that occur in them.
Learning Objectives |
|
The major component of a solution is called the solvent. The minor component of a solution is called the solute. By major and minor we mean whichever component has the greater presence by mass or by moles. Sometimes this becomes confusing, especially with substances with very different molar masses. However, here we will confine the discussion to solutions for which the major component and the minor component are obvious.
Solutions exist for every possible phase of the solute and the solvent. Salt water, for example, is a solution of solid NaCl in liquid water; soda water is a solution of gaseous CO2 in liquid water, while air is a solution of a gaseous solute (O2) in a gaseous solvent (N2). In all cases, however, the overall phase of the solution is the same phase as the solvent.
Example 1 |
|
A solution is made by dissolving 1.00 g of sucrose (C12H22O11) in 100.0 g of liquid water. Identify the solvent and solute in the resulting solution. Solution Either by mass or by moles, the obvious minor component is sucrose, so it is the solute. Water—the majority component—is the solvent. The fact that the resulting solution is the same phase as water also suggests that water is the solvent. Test Yourself A solution is made by dissolving 3.33 g of HCl(g) in 40.0 g of liquid methyl alcohol (CH3OH). Identify the solvent and solute in the resulting solution. Answer solute: HCl(g); solvent: CH3OH |
One important concept of solutions is in defining how much solute is dissolved in a given amount of solvent. This concept is called concentration. Various words are used to describe the relative amounts of solute. Dilute describes a solution that has very little solute, while concentrated describes a solution that has a lot of solute. One problem is that these terms are qualitative; they describe more or less but not exactly how much.
In most cases, only a certain maximum amount of solute can be dissolved in a given amount of solvent. This maximum amount is called the solubility of the solute. It is usually expressed in terms of the amount of solute that can dissolve in 100 g of the solvent at a given temperature. Table 10.2 "Solubilities of Some Ionic Compounds" lists the solubilities of some simple ionic compounds. These solubilities vary widely: NaCl can dissolve up to 31.6 g per 100 g of H2O, while AgCl can dissolve only 0.00019 g per 100 g of H2O.
Table 10.2 Solubilities of Some Ionic Compounds
| Solute | Solubility (g per 100 g of H2O at 25°C) |
|---|---|
| AgCl | 0.00019 |
| CaCO3 | 0.0006 |
| KBr | 70.7 |
| NaCl | 36.1 |
| NaNO3 | 94.6 |
When the maximum amount of solute has been dissolved in a given amount of solvent, we say that the solution is saturated with solute. When less than the maximum amount of solute is dissolved in a given amount of solute, the solution is unsaturated These terms are also qualitative terms because each solute has its own solubility. A solution of 0.00019 g of AgCl per 100 g of H2O may be saturated, but with so little solute dissolved, it is also rather dilute. A solution of 36.1 g of NaCl in 100 g of H2O is also saturated but rather concentrated. Ideally, we need more precise ways of specifying the amount of solute in a solution. We will introduce such ways in Section 10.2 "Quantitative Units of Concentration".
In some circumstances, it is possible to dissolve more than the maximum amount of a solute in a solution. Usually, this happens by heating the solvent, dissolving more solute than would normally dissolve at regular temperatures, and letting the solution cool down slowly and carefully. Such solutions are called supersaturated solutions and are not stable; given an opportunity (such as dropping a crystal of solute in the solution), the excess solute will precipitate from the solution.
It should be obvious that some solutes dissolve in certain solvents but not others. NaCl, for example, dissolves in water but not in vegetable oil. Beeswax dissolves in liquid hexane but not water. What is it that makes a solute soluble in some solvents but not others?
The answer is intermolecular interactions. The intermolecular interactions include London dispersion forces, dipole-dipole interactions, and hydrogen bonding (as described in Chapter 3 "Solids and Liquids"). From experimental studies, it has been determined that if molecules of a solute experience the same intermolecular forces that the solvent does, the solute will likely dissolve in that solvent. So, NaCl—a very polar substance because it is composed of ions—dissolves in water, which is very polar, but not in oil, which is generally nonpolar. Nonpolar wax dissolves in nonpolar hexane but not in polar water. This concept leads to the general rule that “like dissolves like” for predicting whether a solute is soluble in a given solvent. However, this is a general rule, not an absolute statement, so it must be applied with care.
Example 2 |
|
Would I2 be more soluble in CCl4 or H2O? Explain your answer. Solution I2 is nonpolar. Of the two solvents, CCl4 is nonpolar and H2O is polar, so I2 would be expected to be more soluble in CCl4. Test Yourself Would C3H7OH be more soluble in CCl4 or H2O? Explain your answer. Answer H2O because both experience hydrogen bonding |
Key Takeaways |
|
Exercises |
|
Learning Objective |
| Learn to determine specific concentrations with several common units. |
Rather than qualitative terms (Section 10.1 "Some Definitions"), we need quantitative ways to express the amount of solute in a solution; that is, we need specific units of concentration. In this section, we will introduce several common and useful units of concentration.
Molarity (M) is defined as the number of moles of solute divided by the number of liters of solution:
which can be simplified as
As with any mathematical equation, if you know any two quantities, you can calculate the third, unknown, quantity.
For example, suppose you have 0.500 L of solution that has 0.24 mol of NaOH dissolved in it. The concentration of the solution can be calculated as follows:
The concentration of the solution is 0.48 M, which is spoken as “zero point forty-eight molarity” or “zero point forty-eight molar.” If the quantity of the solute is given in mass units, you must convert mass units to mole units before using the definition of molarity to calculate concentration. For example, what is the molar concentration of a solution of 22.4 g of HCl dissolved in 1.56 L? First, convert the mass of solute to moles using the molar mass of HCl (36.5 g/mol):
Now we can use the definition of molarity to determine a concentration:
Example 3 |
|
What is the molarity of a solution made when 32.7 g of NaOH are dissolved to make 445 mL of solution? Solution To use the definition of molarity, both quantities must be converted to the proper units. First, convert the volume units from milliliters to liters: Now we convert the amount of solute to moles, using the molar mass of NaOH, which is 40.0 g/mol: Now we can use the definition of molarity to determine the molar concentration:
Test Yourself What is the molarity of a solution made when 66.2 g of C6H12O6 are dissolved to make 235 mL of solution? Answer 1.57 M |
The definition of molarity can be used to determine the amount of solute or the volume of solution, if the other information is given. Example 4 illustrates this situation.
Example 4 |
|
How many moles of solute are present in 0.108 L of a 0.887 M NaCl solution? Solution We know the volume and the molarity; we can use the definition of molarity to mathematically solve for the amount in moles. Substituting the quantities into the definition of molarity:
We multiply the 0.108 L over to the other side of the equation and multiply the units together; “molarity × liters” equals moles, according to the definition of molarity. So mol NaCl = (0.887 M)(0.108 L) = 0.0958 mol
Test Yourself How many moles of solute are present in 225 mL of a 1.44 M CaCl2 solution? Answer 0.324 mol |
If you need to determine volume, remember the rule that the unknown quantity must be by itself and in the numerator to determine the correct answer. Thus rearrangement of the definition of molarity is required.
Example 5 |
|
What volume of a 2.33 M NaNO3 solution is needed to obtain 0.222 mol of solute? Solution Using the definition of molarity, we have To solve for the number of liters, we bring the 2.33 M over to the right into the denominator, and the number of liters over to the left in the numerator. We now have Dividing, the volume is 0.0953 L = 95.3 mL.
Test Yourself What volume of a 0.570 M K2SO4 solution is needed to obtain 0.872 mol of solute?
Answer 1.53 L |
A similar unit of concentration is molality (m), which is defined as the number of moles of solute per kilogram of solvent, not per liter of solution:
Mathematical manipulation of molality is the same as with molarity.
Another way to specify an amount is percentage composition by mass (or mass percentage, % m/m). It is defined as follows:
It is not uncommon to see this unit used on commercial products (Figure 10.1 "Concentration in Commercial Applications").
Example 6 |
|
What is the mass percentage of Fe in a piece of metal with 87.9 g of Fe in a 113 g sample? Solution Using the definition of mass percentage, we have
Test Yourself What is the mass percentage of H2O2 in a solution with 1.67 g of H2O2 in a 55.5 g sample? Answer 3.01% |
Related concentration units are parts per thousand (ppth), parts per million (ppm), and parts per billion (ppb). Parts per thousand is defined as follows:
There are similar definitions for parts per million and parts per billion:
and Each unit is used for progressively lower and lower concentrations. The two masses must be expressed in the same unit of mass, so conversions may be necessary.
Example 7 |
|
If there is 0.6 g of Pb present in 277 g of solution, what is the Pb concentration in parts per thousand? Solution Use the definition of parts per thousand to determine the concentration. Substituting Test Yourself If there is 0.551 mg of As in 348 g of solution, what is the As concentration in ppm? Answer 1.58 ppm |
As with molarity and molality, algebraic rearrangements may be necessary to answer certain questions.
Example 8 |
|
The concentration of Cl– ion in a sample of H2O is 15.0 ppm. What mass of Cl– ion is present in 240.0 mL of H2O, which has a density of 1.00 g/mL? Solution First, use the density of H2O to determine the mass of the sample: Now we can use the definition of ppm: Rearranging to solve for the mass of solute,
Test Yourself The concentration of Fe3+ ion in a sample of H2O is 335.0 ppm. What mass of Fe3+ ion is present in 3,450 mL of H2O, which has a density of 1.00 g/mL? Answer 1.16 g
|
For ionic solutions, we need to differentiate between the concentration of the salt versus the concentration of each individual ion. Because the ions in ionic compounds go their own way when a compound is dissolved in a solution, the resulting concentration of the ion may be different from the concentration of the complete salt. For example, if 1 M NaCl were prepared, the solution could also be described as a solution of 1 M Na+(aq) and 1 M Cl−(aq) because there is one Na+ ion and one Cl− ion per formula unit of the salt. However, if the solution were 1 M CaCl2, there are two Cl−(aq) ions for every formula unit dissolved, so the concentration of Cl−(aq) would be 2 M, not 1 M.
In addition, the total ion concentration is the sum of the individual ion concentrations. Thus for the 1 M NaCl, the total ion concentration is 2 M; for the 1 M CaCl2, the total ion concentration is 3 M.
Key Takeaway |
| Quantitative units of concentration include molarity, molality, mass percentage, parts per thousand, parts per million, and parts per billion. |
Exercises |
|
Learning Objective |
| Learn how to dilute and concentrate solutions. |
Often, a worker will need to change the concentration of a solution by changing the amount of solvent. Dilution is the addition of solvent, which decreases the concentration of the solute in the solution. Concentration is the removal of solvent, which increases the concentration of the solute in the solution. (Do not confuse the two uses of the word concentration here!)
In both dilution and concentration, the amount of solute stays the same. This gives us a way to calculate what the new solution volume must be for the desired concentration of solute. From the definition of molarity,
we can solve for the number of moles of solute:
moles of solute = (molarity)(liters of solution)
A simpler way of writing this is to use M to represent molarity and V to represent volume. So the equation becomes
moles of solute = MV
Because this quantity does not change before and after the change in concentration, the product MV must be the same before and after the concentration change. Using numbers to represent the initial and final conditions, we have
M1V1 = M2V2
as the dilution equation. The volumes must be expressed in the same units. Note that this equation gives only the initial and final conditions, not the amount of the change. The amount of change is determined by subtraction.
Example 9 |
|
If 25.0 mL of a 2.19 M solution are diluted to 72.8 mL, what is the final concentration? Solution It does not matter which set of conditions is labeled 1 or 2, as long as the conditions are paired together properly. Using the dilution equation, we have (2.19 M)(25.0 mL) = M2(72.8 mL)Solving for the second concentration (noting that the milliliter units cancel), M2 = 0.752 MThe concentration of the solution has decreased. In going from 25.0 mL to 72.8 mL, 72.8 − 25.0 = 47.8 mL of solvent must be added. Test Yourself A 0.885 M solution of KBr whose initial volume is 76.5 mL has more water added until its concentration is 0.500 M. What is the new volume of the solution? Answer 135.4 mL |
Concentrating solutions involves removing solvent. Usually this is done by evaporating or boiling, assuming that the heat of boiling does not affect the solute. The dilution equation is used in these circumstances as well.
Chemistry Is Everywhere: Preparing IV SolutionsIn a hospital emergency room, a physician orders an intravenous (IV) delivery of 100 mL of 0.5% KCl for a patient suffering from hypokalemia (low potassium levels). Does an aide run to a supply cabinet and take out an IV bag containing this concentration of KCl? Not likely. It is more probable that the aide must make the proper solution from an IV bag of sterile solution and a more concentrated, sterile solution, called a stock solution, of KCl. The aide is expected to use a syringe to draw up some stock solution and inject it into the waiting IV bag and dilute it to the proper concentration. Thus the aide must perform a dilution calculation. If the stock solution is 10.0% KCl and the final volume and concentration need to be 100 mL and 0.50%, respectively, then it is an easy calculation to determine how much stock solution to use: (10%)V1 = (0.50%)(100 mL) V1 = 5 mLOf course, the addition of the stock solution affects the total volume of the diluted solution, but the final concentration is likely close enough even for medical purposes. Medical and pharmaceutical personnel are constantly dealing with dosages that require concentration measurements and dilutions. It is an important responsibility: calculating the wrong dose can be useless, harmful, or even fatal! |
Key Takeaway |
| Calculate the new concentration or volume for a dilution or concentration of a solution. |
Exercises |
|
Learning Objective |
| Apply concentration units as conversion factors. |
Concentration can be a conversion factor between the amount of solute and the amount of solution or solvent (depending on the definition of the concentration unit). As such, concentrations can be useful in a variety of stoichiometry problems. In many cases, it is best to use the original definition of the concentration unit; it is that definition that provides the conversion factor.
A simple example of using a concentration unit as a conversion factor is one in which we use the definition of the concentration unit and rearrange; we can do the calculation again as a unit conversion, rather than as a definition. For example, suppose we ask how many moles of solute are present in 0.108 L of a 0.887 M NaCl solution. Because 0.887 M means 0.887 mol/L, we can use this second expression for the concentration as a conversion factor:
(There is an understood 1 in the denominator of the conversion factor.) If we used the definition approach, we get the same answer, but now we are using conversion factor skills. Like any other conversion factor that relates two different types of units, the reciprocal of the concentration can be also used as a conversion factor.
Example 10 |
|
Using concentration as a conversion factor, how many liters of 2.35 M CuSO4 are needed to obtain 4.88 mol of CuSO4? Solution This is a one-step conversion, but the concentration must be written as the reciprocal for the units to work out:
Test Yourself Using concentration as a conversion factor, how many liters of 0.0444 M CH2O are needed to obtain 0.0773 mol of CH2O? Answer 1.74 L |
Of course, once quantities in moles are available, another conversion can give the mass of the substance, using molar mass as a conversion factor.
Example 11 |
|
What mass of solute is present in 0.765 L of 1.93 M NaOH? Solution This is a two-step conversion, first using concentration as a conversion factor to determine the number of moles and then the molar mass of NaOH (40.0 g/mol) to convert to mass: Test Yourself What mass of solute is present in 1.08 L of 0.0578 M H2SO4? Answer 6.12 g
|
More complex stoichiometry problems using balanced chemical reactions can also use concentrations as conversion factors. For example, suppose the following equation represents a chemical reaction:
2AgNO3(aq) + CaCl2(aq) → 2AgCl(s) + Ca(NO3)2(aq)
If we wanted to know what volume of 0.555 M CaCl2 would react with 1.25 mol of AgNO3, we first use the balanced chemical equation to determine the number of moles of CaCl2 that would react and then use concentration to convert to liters of solution:
This can be extended by starting with the mass of one reactant, instead of moles of a reactant.
Example 12 |
|
What volume of 0.0995 M Al(NO3)3 will react with 3.66 g of Ag according to the following chemical equation? 3Ag(s) + Al(NO3)3(aq) → 3AgNO3 + Al(s)
Solution Here, we first must convert the mass of Ag to moles before using the balanced chemical equation and then the definition of molarity as a conversion factor: The strikeouts show how the units cancel. Test Yourself What volume of 0.512 M NaOH will react with 17.9 g of H2C2O4(s) according to the following chemical equation? H2C2O4(s) + 2NaOH(aq) → Na2C2O4(aq) + 2H2O(ℓ)
Answer 0.777 L |
We can extend our skills even further by recognizing that we can relate quantities of one solution to quantities of another solution. Knowing the volume and concentration of a solution containing one reactant, we can determine how much of another solution of another reactant will be needed using the balanced chemical equation.
Example 13 |
|
A student takes a precisely measured sample, called an aliquot, of 10.00 mL of a solution of FeCl3. The student carefully adds 0.1074 M Na2C2O4 until all the Fe3+(aq) has precipitated as Fe2(C2O4)3(s). Using a precisely measured tube called a burette, the student finds that 9.04 mL of the Na2C2O4 solution was added to completely precipitate the Fe3+(aq). What was the concentration of the FeCl3 in the original solution? (A precisely measured experiment like this, which is meant to determine the amount of a substance in a sample, is called a titration.) The balanced chemical equation is as follows: 2FeCl3(aq) + 3Na2C2O4(aq) → Fe2(C2O4)3(s) + 6NaCl(aq)
Solution First we need to determine the number of moles of Na2C2O4 that reacted. We will convert the volume to liters and then use the concentration of the solution as a conversion factor: Now we will use the balanced chemical equation to determine the number of moles of Fe3+(aq) that were present in the initial aliquot: Then we determine the concentration of FeCl3 in the original solution. Converting 10.00 mL into liters (0.01000 L), we use the definition of molarity directly: Test Yourself A student titrates 25.00 mL of H3PO4 with 0.0987 M KOH. She uses 54.06 mL to complete the chemical reaction. What is the concentration of H3PO4? H3PO4(aq) + 3KOH(aq) → K3PO4(aq) + 3H2O
Answer 0.0711 M |
We have used molarity exclusively as the concentration of interest, but that will not always be the case. The next example shows a different concentration unit being used.
Example 14 |
|
H2O2 is used to determine the amount of Mn according to this balanced chemical equation: 2MnO4−(aq) + 5H2O2(aq) + 6H+(aq) → 2Mn2+(aq) + 5O2(g) + 8H2O(ℓ) What mass of 3.00% m/m H2O2 solution is needed to react with 0.355 mol of MnO4−(aq)? Solution Because we are given an initial amount in moles, all we need to do is use the balanced chemical equation to determine the number of moles of H2O2 and then convert to find the mass of H2O2. Knowing that the H2O2 solution is 3.00% by mass, we can determine the mass of solution needed: The first conversion factor comes from the balanced chemical equation, the second conversion factor is the molar mass of H2O2, and the third conversion factor comes from the definition of percentage concentration by mass. Test Yourself Use the balanced chemical reaction for MnO4− and H2O2 to determine what mass of O2 is produced if 258 g of 3.00% m/m H2O2 is reacted with MnO4−. Answer 7.28 g |
Key Takeaway |
| Know how to apply concentration units as conversion factors. |
Exercises |
|
Learning Objectives |
|
The properties of solutions are very similar to the properties of their respective pure solvents. This makes sense because the majority of the solution is the solvent. However, some of the properties of solutions differ from pure solvents in measurable and predictable ways. The differences are proportional to the fraction that the solute particles occupy in the solution. These properties are called colligative properties; the word colligative comes from the Greek word meaning “related to the number,” implying that these properties are related to the number of solute particles, not their identities.
Before we introduce the first colligative property, we need to introduce a new concentration unit. The mole fraction of the ith component in a solution, χi, is the number of moles of that component divided by the total number of moles in the sample:
(χ is the lowercase Greek letter chi.) The mole fraction is always a number between 0 and 1 (inclusive) and has no units; it is just a number.
Example 15 |
|
A solution is made by mixing 12.0 g of C10H8 in 45.0 g of C6H6. What is the mole fraction of C10H8 in the solution? Solution We need to determine the number of moles of each substance, add them together to get the total number of moles, and then divide to determine the mole fraction of C10H8. The number of moles of C10H8 is as follows: The number of moles of C6H6 is as follows: The total number of moles is 0.0936 mol + 0.576 mol = 0.670 mol Now we can calculate the mole fraction of C10H8: The mole fraction is a number between 0 and 1 and is unitless. Test Yourself A solution is made by mixing 33.8 g of CH3OH in 50.0 g of H2O. What is the mole fraction of CH3OH in the solution? Answer 0.275 |
A useful thing to note is that the sum of the mole fractions of all substances in a mixture equals 1. Thus the mole fraction of C6H6 in Example 15 could be calculated by evaluating the definition of mole fraction a second time, or—because there are only two substances in this particular mixture—we can subtract the mole fraction of the C10H8 from 1 to get the mole fraction of C6H6.
Now that this new concentration unit has been introduced, the first colligative property can be considered. As was mentioned in Chapter 3 "Solids and Liquids", all pure liquids have a characteristic vapor pressure in equilibrium with the liquid phase, the partial pressure of which is dependent on temperature. Solutions, however, have a lower vapor pressure than the pure solvent has, and the amount of lowering is dependent on the fraction of solute particles, as long as the solute itself does not have a significant vapor pressure (the term nonvolatile is used to describe such solutes). This colligative property is called vapor pressure depression (or lowering). The actual vapor pressure of the solution can be calculated as follows:
where Psoln is the vapor pressure of the solution, χsolv is the mole fraction of the solvent particles, and is the vapor pressure of the pure solvent at that temperature (which is data that must be provided). This equation is known as Raoult’s law (the approximate pronunciation is rah-OOLT). Vapor pressure depression is rationalized by presuming that solute particles take positions at the surface in place of solvent particles, so not as many solvent particles can evaporate.
Example 16 |
|
A solution is made by mixing 12.0 g of C10H8 in 45.0 g of C6H6. If the vapor pressure of pure C6H6 is 95.3 torr, what is the vapor pressure of the solution? Solution This is the same solution that was in Example 15, but here we need the mole fraction of C6H6. The number of moles of C10H8 is as follows: The number of moles of C6H6 is as follows: So the total number of moles is 0.0936 mol + 0.576 mol = 0.670 molNow we can calculate the mole fraction of C6H6: (The mole fraction of C10H8 calculated in Example 15 plus the mole fraction of C6H6 equals 1, which is mathematically required by the definition of mole fraction.) Now we can use Raoult’s law to determine the vapor pressure in equilibrium with the solution: Psoln = (0.860)(95.3 torr) = 82.0 torrThe solution has a lower vapor pressure than the pure solvent. Test Yourself A solution is made by mixing 33.8 g of C6H12O6 in 50.0 g of H2O. If the vapor pressure of pure water is 25.7 torr, what is the vapor pressure of the solution? Answer 24.1 torr |
Two colligative properties are related to solution concentration as expressed in molality. As a review, recall the definition of molality:
Because the vapor pressure of a solution with a nonvolatile solute is depressed compared to that of the pure solvent, it requires a higher temperature for the solution’s vapor pressure to reach 1.00 atm (760 torr). Recall that this is the definition of the normal boiling point: the temperature at which the vapor pressure of the liquid equals 1.00 atm. As such, the normal boiling point of the solution is higher than that of the pure solvent. This property is called boiling point elevation.
The change in boiling point (ΔTb) is easily calculated:
ΔTb = mKb
where m is the molality of the solution and Kb is called the boiling point elevation constant, which is a characteristic of the solvent. Several boiling point elevation constants (as well as boiling point temperatures) are listed in Table 10.3 "Boiling Point Data for Various Liquids".
Table 10.3 Boiling Point Data for Various Liquids
| Liquid | Boiling Point (°C) | Kb (°C/m) |
|---|---|---|
| HC2H3O2 | 117.90 | 3.07 |
| C6H6 | 80.10 | 2.53 |
| CCl4 | 76.8 | 4.95 |
| H2O | 100.00 | 0.512 |
Remember that what is initially calculated is the change in boiling point temperature, not the new boiling point temperature. Once the change in boiling point temperature is calculated, it must be added to the boiling point of the pure solvent—because boiling points are always elevated—to get the boiling point of the solution.
Example 17 |
|
What is the boiling point of a 2.50 m solution of C6H4Cl2 in CCl4? Assume that C6H4Cl2 is not volatile. Solution Using the equation for the boiling point elevation, ΔTb = (2.50 m)(4.95°C/m) = 12.4°C
Note how the molality units have canceled. However, we are not finished. We have calculated the change in the boiling point temperature, not the final boiling point temperature. If the boiling point goes up by 12.4°C, we need to add this to the normal boiling point of CCl4 to get the new boiling point of the solution: TBP = 76.8°C + 12.4°C = 89.2°C The boiling point of the solution is predicted to be 89.2°C. Test Yourself What is the boiling point of a 6.95 m solution of C12H22O11 in H2O? Answer 103.6°C |
The boiling point of a solution is higher than the boiling point of the pure solvent, but the opposite occurs with the freezing point. The freezing point of a solution is lower than the freezing point of the pure solvent. Think of this by assuming that solute particles interfere with solvent particles coming together to make a solid, so it takes a lower temperature to get the solvent particles to solidify. This is called freezing point depression.
The equation to calculate the change in the freezing point for a solution is similar to the equation for the boiling point elevation:
ΔTf = mKf
where m is the molality of the solution and Kf is called the freezing point depression constant, which is also a characteristic of the solvent. Several freezing point depression constants (as well as freezing point temperatures) are listed in Table 10.4 "Freezing Point Data for Various Liquids".
Table 10.4 Freezing Point Data for Various Liquids
| Liquid | Freezing Point (°C) | Kf (°C/m) |
|---|---|---|
| HC2H3O2 | 16.60 | 3.90 |
| C6H6 | 5.51 | 4.90 |
| C6H12 | 6.4 | 20.2 |
| C10H8 | 80.2 | 6.8 |
| H2O | 0.00 | 1.86 |
Remember that this equation calculates the change in the freezing point, not the new freezing point. What is calculated needs to be subtracted from the normal freezing point of the solvent because freezing points always go down.
Example 18 |
|
What is the freezing point of a 1.77 m solution of CBr4 in C6H6? Solution We use the equation to calculate the change in the freezing point and then subtract this number from the normal freezing point of C6H6 to get the freezing point of the solution: ΔTf = (1.77 m)(4.90°C/m) = 8.67°CNow we subtract this number from the normal freezing point of C6H6, which is 5.51°C: 5.51 − 8.67 = −3.16°CThe freezing point of the solution is −3.16°C. Test Yourself What is the freezing point of a 3.05 m solution of CBr4 in C10H8? Answer 59.5°C |
Freezing point depression is one colligative property we use in everyday life. Many antifreezes used in automobile radiators use solutions that have a lower freezing point than normal so that automobile engines can operate at subfreezing temperatures. We also take advantage of freezing point depression when we sprinkle various compounds on ice to thaw it in the winter for safety (Figure 10.2 "Salt and Safety"). The compounds make solutions that have a lower freezing point, so rather than forming slippery ice, any ice is liquefied and runs off, leaving a safer pavement behind.
Before we introduce the final colligative property, we need to present a new concept. A semipermeable membrane is a thin membrane that will pass certain small molecules but not others. A thin sheet of cellophane, for example, acts as a semipermeable membrane.
Consider the system in Figure 10.3 "Osmosis"a. A semipermeable membrane separates two solutions having the different concentrations marked. Curiously, this situation is not stable; there is a tendency for water molecules to move from the dilute side (on the left) to the concentrated side (on the right) until the concentrations are equalized, as in Figure 10.3 "Osmosis" (b). This tendency is called osmosis. In osmosis, the solute remains in its original side of the system; only solvent molecules move through the semipermeable membrane. In the end, the two sides of the system will have different volumes. Because a column of liquid exerts a pressure, there is a pressure difference Π on the two sides of the system that is proportional to the height of the taller column. This pressure difference is called the osmotic pressure, which is a colligative property.
Figure 10.3 Osmosis
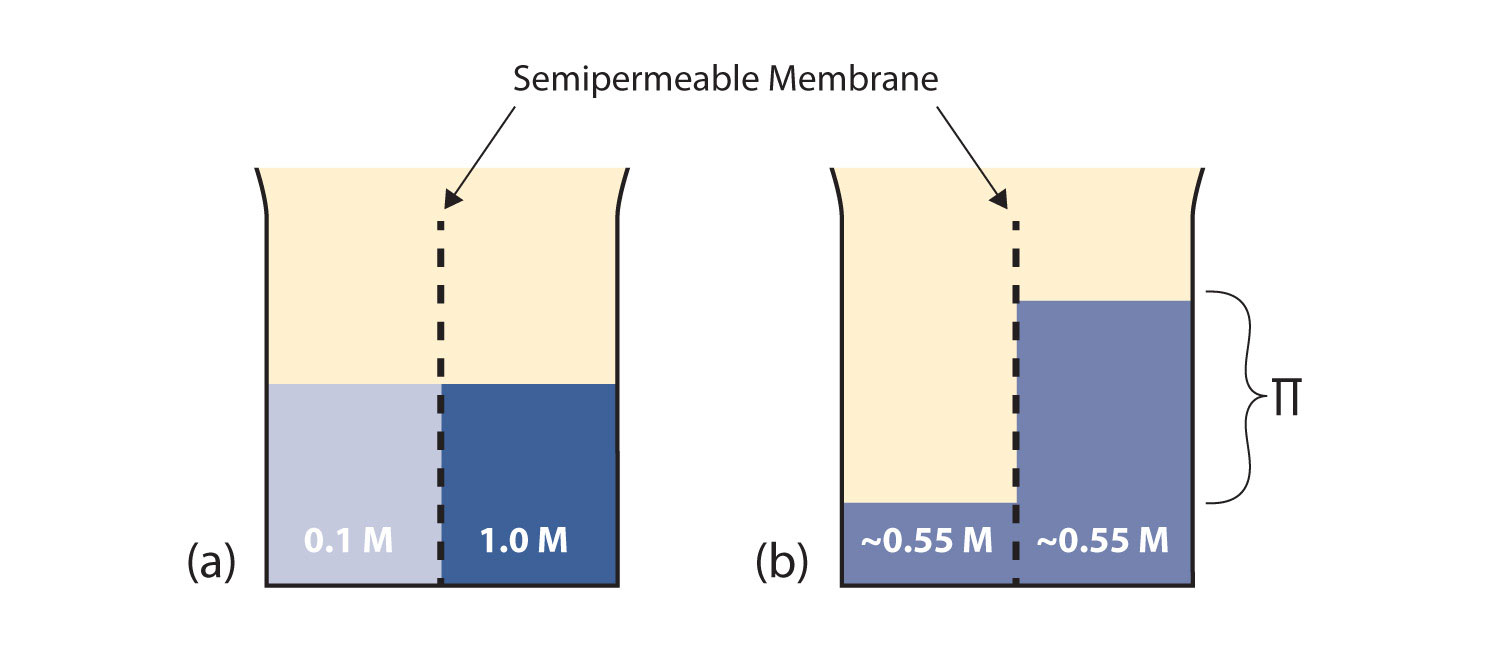
(a) Two solutions of differing concentrations are placed on either side of a semipermeable membrane. (b) When osmosis occurs, solvent molecules selectively pass through the membrane from the dilute solution to the concentrated solution, diluting it until the two concentrations are the same. The pressure exerted by the different height of the solution on the right is called the osmotic pressure.
The osmotic pressure of a solution is easy to calculate:
Π = MRT
where Π is the osmotic pressure of a solution, M is the molarity of the solution, R is the ideal gas law constant, and T is the absolute temperature. This equation is reminiscent of the ideal gas law we considered in Chapter 9 "Gases".
Example 19 |
|
What is the osmotic pressure of a 0.333 M solution of C6H12O6 at 25°C? Solution First we need to convert our temperature to kelvins: T = 25 + 273 = 298 KNow we can substitute into the equation for osmotic pressure, recalling the value for R: The units may not make sense until we realize that molarity is defined as moles per liter: Now we see that the moles, liters, and kelvins cancel, leaving atmospheres, which is a unit of pressure. Solving, Π = 8.14 atmThis is a substantial pressure! It is the equivalent of a column of water 84 m tall. Test Yourself What is the osmotic pressure of a 0.0522 M solution of C12H22O11 at 55°C? Answer 1.40 atm |
Osmotic pressure is important in biological systems because cell walls are semipermeable membranes. In particular, when a person is receiving intravenous (IV) fluids, the osmotic pressure of the fluid needs to be approximately the same as blood serum; otherwise bad things can happen. Figure 10.4 "Osmotic Pressure and Red Blood Cells" shows three red blood cells: Figure 10.4 "Osmotic Pressure and Red Blood Cells"a shows a healthy red blood cell. Figure 10.4 "Osmotic Pressure and Red Blood Cells"b shows a red blood cell that has been exposed to a lower concentration than normal blood serum (a so-called hypotonic solution); the cell has plumped up as solvent moves into the cell to dilute the solutes inside. Figure 10.4 "Osmotic Pressure and Red Blood Cells"c shows a red blood cell exposed to a higher concentration than normal blood serum (hypertonic); water leaves the red blood cell, so it collapses onto itself. Only when the solutions inside and outside the cell are the same (isotonic) will the red blood cell be able to do its job.
Figure 10.4 Osmotic Pressure and Red Blood Cells
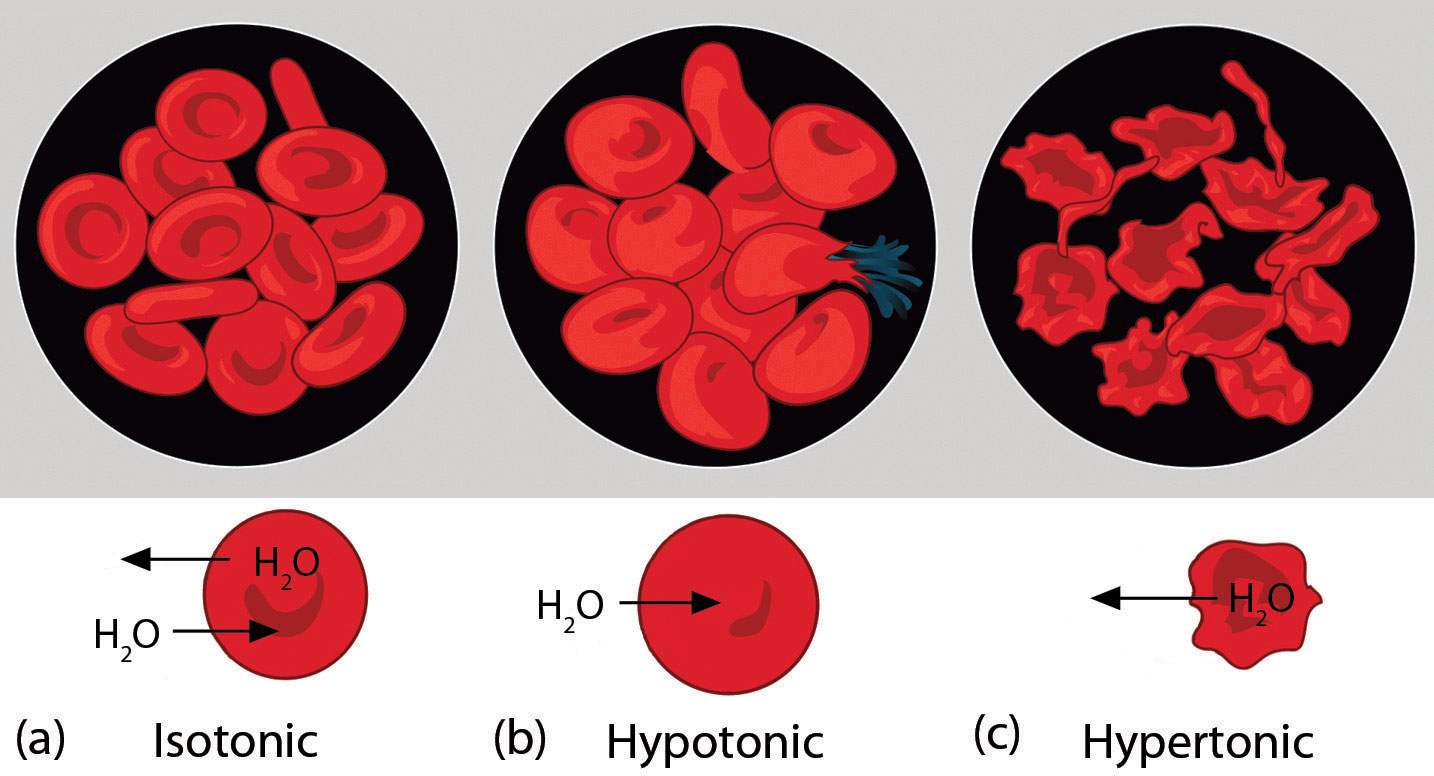
(a) This is what a normal red blood cell looks like. (b) When a red blood cell is exposed to a hypotonic solution, solvent goes through the cell membrane and dilutes the inside of the cell. (c) When a red blood cell is exposed to a hypertonic solution, solvent goes from the cell to the surrounding solution, diluting the hypertonic solution and collapsing the cell. Neither of these last two cases is desirable, so IV solutions must be isotonic with blood serum to not cause deleterious effects.
Osmotic pressure is also the reason you should not drink seawater if you’re stranded in a lifeboat on an ocean; seawater has a higher osmotic pressure than most of the fluids in your body. You can drink the water, but ingesting it will pull water out of your cells as osmosis works to dilute the seawater. Ironically, your cells will die of thirst, and you will also die. (It is OK to drink the water if you are stranded on a body of freshwater, at least from an osmotic pressure perspective.) Osmotic pressure is also thought to be important—in addition to capillary action—in getting water to the tops of tall trees.
Key Takeaways |
|
Exercises |
|
Learning Objective |
| Determine the colligative properties of solutions of ionic solutes. |
In Section 10.5 "Colligative Properties of Solutions", we considered the colligative properties of solutions with molecular solutes. What about solutions with ionic solutes? Do they exhibit colligative properties?
There is a complicating factor: ionic solutes separate into ions when they dissolve. This increases the total number of particles dissolved in solution and increases the impact on the resulting colligative property. Historically, this greater-than-expected impact on colligative properties was one main piece of evidence for ionic compounds separating into ions (increased electrical conductivity was another piece of evidence).
For example, when NaCl dissolves, it separates into two ions:
NaCl(s) → Na+(aq) + Cl−(aq)
This means that a 1 M solution of NaCl actually has a net particle concentration of 2 M. The observed colligative property will then be twice as large as expected for a 1 M solution.
It is easy to incorporate this concept into our equations to calculate the respective colligative property. We define the van’t Hoff factor (i) as the number of particles each solute formula unit breaks apart into when it dissolves. Previously, we have always tacitly assumed that the van’t Hoff factor is simply 1. But for some ionic compounds, i is not 1, as shown in Table 10.5 "Ideal van’t Hoff Factors for Ionic Compounds".
Table 10.5 Ideal van’t Hoff Factors for Ionic Compounds
| Compound | i |
|---|---|
| NaCl | 2 |
| KBr | 2 |
| LiNO3 | 2 |
| CaCl2 | 3 |
| Mg(C2H3O2)2 | 3 |
| FeCl3 | 4 |
| Al2(SO4)3 | 5 |
The ideal van’t Hoff factor is equal to the number of ions that form when an ionic compound dissolves.
Example 20 |
|
Predict the van’t Hoff factor for Sr(OH)2. Solution When Sr(OH)2 dissolves, it separates into one Sr2+ ion and two OH− ions: Sr(OH)2 → Sr2+(aq) + 2OH−(aq)Because it breaks up into three ions, its van’t Hoff factor is 3. Test Yourself What is the van’t Hoff factor for Fe(NO3)3? Answer 4 |
It is the “ideal” van’t Hoff factor because this is what we expect from the ionic formula. However, this factor is usually correct only for dilute solutions (solutions less than 0.001 M). At concentrations greater than 0.001 M, there are enough interactions between ions of opposite charge that the net concentration of the ions is less than expected—sometimes significantly. The actual van’t Hoff factor is thus less than the ideal one. Here, we will use ideal van’t Hoff factors.
Revised equations to calculate the effect of ionization are then easily produced:
ΔTb = imKb ΔTf = imKg Π = iMRT
where all variables have been previously defined. To calculate vapor pressure depression according to Raoult’s law, the mole fraction of solvent particles must be recalculated to take into account the increased number of particles formed on ionization.
Example 21 |
|
Determine the freezing point of a 1.77 m solution of NaCl in H2O. Solution For NaCl, we need to remember to include the van’t Hoff factor, which is 2. Otherwise, the calculation of the freezing point is straightforward: ΔTf = (2)(1.77 m)(1.86°C/m) = 6.58°CThis represents the change in the freezing point, which is decreasing. So we have to subtract this change from the normal freezing point of water, 0.00°C: 0.00 − 6.58 = −6.58°C
Test Yourself Determine the boiling point of a 0.887 m solution of CaCl2 in H2O. Answer 101.36°C |
Food and Drink App: Salting Pasta Cooking WaterWhen cooking dried pasta, many recipes call for salting the water before cooking the pasta. Some argue—with colligative properties on their side—that adding salt to the water raises the boiling point, thus cooking the pasta faster. Is there any truth to this? To judge the veracity of this claim, we can calculate how much salt should be added to the water to raise the boiling temperature by 1.0°C, with the presumption that dried pasta cooks noticeably faster at 101°C than at 100°C (although a 1° difference may make only a negligible change in cooking times). We can calculate the molality that the water should have: 1.0°C = m(0.512°C/m) m = 1.95We have ignored the van’t Hoff factor in our estimation because this obviously is not a dilute solution. Let us further assume that we are using 4 L of water (which is very close to 4 qt, which in turn equals 1 gal). Because 4 L of water is about 4 kg (it is actually slightly less at 100°C), we can determine how much salt (NaCl) to add: This is just over 1 lb of salt and is equivalent to nearly 1 cup in the kitchen. In your experience, do you add almost a cup of salt to a pot of water to make pasta? Certainly not! A few pinches, perhaps one-fourth of a teaspoon, but not almost a cup! It is obvious that the little amount of salt that most people add to their pasta water is not going to significantly raise the boiling point of the water. So why do people add some salt to boiling water? There are several possible reasons, the most obvious of which is taste: adding salt adds a little bit of salt flavor to the pasta. It cannot be much because most of the salt remains in the water, not in the cooked pasta. However, it may be enough to detect with our taste buds. The other obvious reason is habit; recipes tell us to add salt, so we do, even if there is little scientific or culinary reason to do so. |
Key Takeaways |
|
Exercises |
|
Additional Exercises |
|
Library Info and Research Help | reflibrarian@hostos.cuny.edu (718) 518-4215
Loans or Fines | circ@hostos.cuny.edu (718) 518-4222
475 Grand Concourse (A Building), Room 308, Bronx, NY 10451
