Adapted by Nelson Nuñez-Rodriguez
Conditions of Use:

Unless otherwise noted, this work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
Chapters derived from:
By David W. Ball
 Attribution-NonCommercial-ShareAlike
Attribution-NonCommercial-ShareAlike
CC BY-NC-SA
Click on the printer icon at the bottom of the screen
![]()
Make sure that your printout includes all content from the page. If it doesn't, try opening this guide in a different browser and printing from there (sometimes Internet Explorer works better, sometimes Chrome, sometimes Firefox, etc.).
If the above process produces printouts with errors or overlapping text or images, try this method:
Opening EssayIt takes energy to launch a spaceship into space. If it takes 1 energy unit to warm 0.25 g of water by 1°C, then it takes over 15,100 energy units to put that 0.25 g of water into earth orbit. The most powerful engines designed to lift rockets into space were part of the Saturn V rocket, that was built by the National Aeronautics and Space Administration (NASA). The rocket had three stages, with the first stage having the capability of launching about 3.5 million kg of mass. About 2.3 million kg was the actual fuel for the first stage; rockets in space have the unpleasant task of having to take their own chemicals with them to provide thrust. Having to carry its own fuel puts a lot of mass burden on an engine in space. This is why NASA is developing other types of engines to minimize fuel mass. An ion thruster uses xenon atoms that have had at least one electron removed from their atoms. The resulting ions can be accelerated by electric fields, causing a thrust. Because xenon atoms are very large for atoms, the thrusting efficiency is high even though the actual thrust is low. Because of this, ion engines are useful only in space.
Ion drives have low thrust but high efficiency. They have already been used on several space missions, including NASA’s Deep Space 1 spacecraft and Japan’s Hayabusa asteroid sampling probe. Source: Photo courtesy of NASA, http://commons.wikimedia.org/wiki/File:Ion_Engine_Test_Firing_-_GPN-2000-000482.jpg. |
Energy is a very important quantity in science and the world around us. Although most of our energy ultimately comes from the sun, much of the energy we use on a daily basis is rooted in chemical reactions. The gasoline in your car, the electricity in your house, the food in your diet—all provide substances for chemical reactions to provide energy (gasoline, food) or are produced from chemical reactions (electricity, about 50% of which is generated by burning coal). As such, it is only natural that the study of chemistry involves energy.
Learning Objectives |
|
Energy is the ability to do work. Think about it: when you have a lot of energy, you can do a lot of work; but if you’re low on energy, you don’t want to do much work. Work (w) itself is defined as a force (F) operating over a distance (Δx):
w = F × Δx
In SI, force has units of newtons (N), while distance has units of meters. Therefore, work has units of N·m. This compound unit is redefined as a joule (J):
1 joule = 1 newton·meter 1 J = 1 N·m
Because energy is the ability to do work, energy is also measured in joules. This is the primary unit of energy we will use here.
How much is 1 J? It is enough to warm up about one-fourth of a gram of water by 1°C. It takes about 12,000 J to warm a cup of coffee from room temperature to 50°C. So a joule is not a lot of energy. It will not be uncommon to measure energies in thousands of joules, so the kilojoule (kJ) is a common unit of energy, with 1 kJ equal to 1,000 J.
An older—but still common—unit of energy is the calorie. The calorie (cal) was originally defined in terms of warming up a given quantity of water. The modern definition of calorie equates it to joules:
1 cal = 4.184 J
One area where the calorie is used is in nutrition. Energy contents of foods are often expressed in calories. However, the calorie unit used for foods is actually the kilocalorie (kcal). Most foods indicate this by spelling the word with a capital C—Calorie.
Example 1 |
|
If a food label states that one serving has 38 Cal. How many joules is this? Solution We recognize that with a capital C, the Calories unit is actually kilocalories. To determine the number of joules, we convert first from kilocalories to calories (using the definition of the kilo- prefix) and then from calories to joules (using the relationship between calories and joules). So Test Yourself A serving of breakfast cereal usually has 110 Cal. How many joules of energy is this? Answer 460,000 J |
In the study of energy, we use the term system to describe the part of the universe under study: a beaker, a flask, or a container whose contents are being observed and measured. An isolated system is a system that does not allow a transfer of energy or matter into or out of the system. A good approximation of an isolated system is a closed, insulated thermos-type bottle. The fact that the thermos-type bottle is closed keeps matter from moving in or out, and the fact that it is insulated keeps energy from moving in or out.
One of the fundamental ideas about the total energy of an isolated system is that is does not increase or decrease. When this happens to a quantity, we say that the quantity is conserved. The statement that the total energy of an isolated system does not change is called the law of conservation of energy. As a scientific law, this concept occupies the highest level of understanding we have about the natural universe.
Key Takeaways |
|
Exercises |
|
Learning Objectives |
|
We have already defined work as a force acting through a distance. It turns out that there are other equivalent definitions of work that are also important in chemistry.
When a certain volume of a gas expands, it works against an external pressure to expand (Figure 2.2 "Volume versus Pressure"). That is, the gas must perform work. Assuming that the external pressure Pext is constant, the amount of work done by the gas is given by the equation
w = −Pext × ΔV
where ΔV is the change in volume of the gas. This term is always the final volume minus the initial volume,
ΔV = Vfinal − Vinitial
and can be positive or negative, depending on whether Vfinal is larger (is expanding) or smaller (is contracting) than Vinitial. The negative sign in the equation for work is important and implies that as volume expands (ΔV is positive), the gas in the system is losing energy as work. On the other hand, if the gas is contracting, ΔV is negative, and the two negative signs make the work positive, so energy is being added to the system.
Figure 2.1 Volume versus Pressure
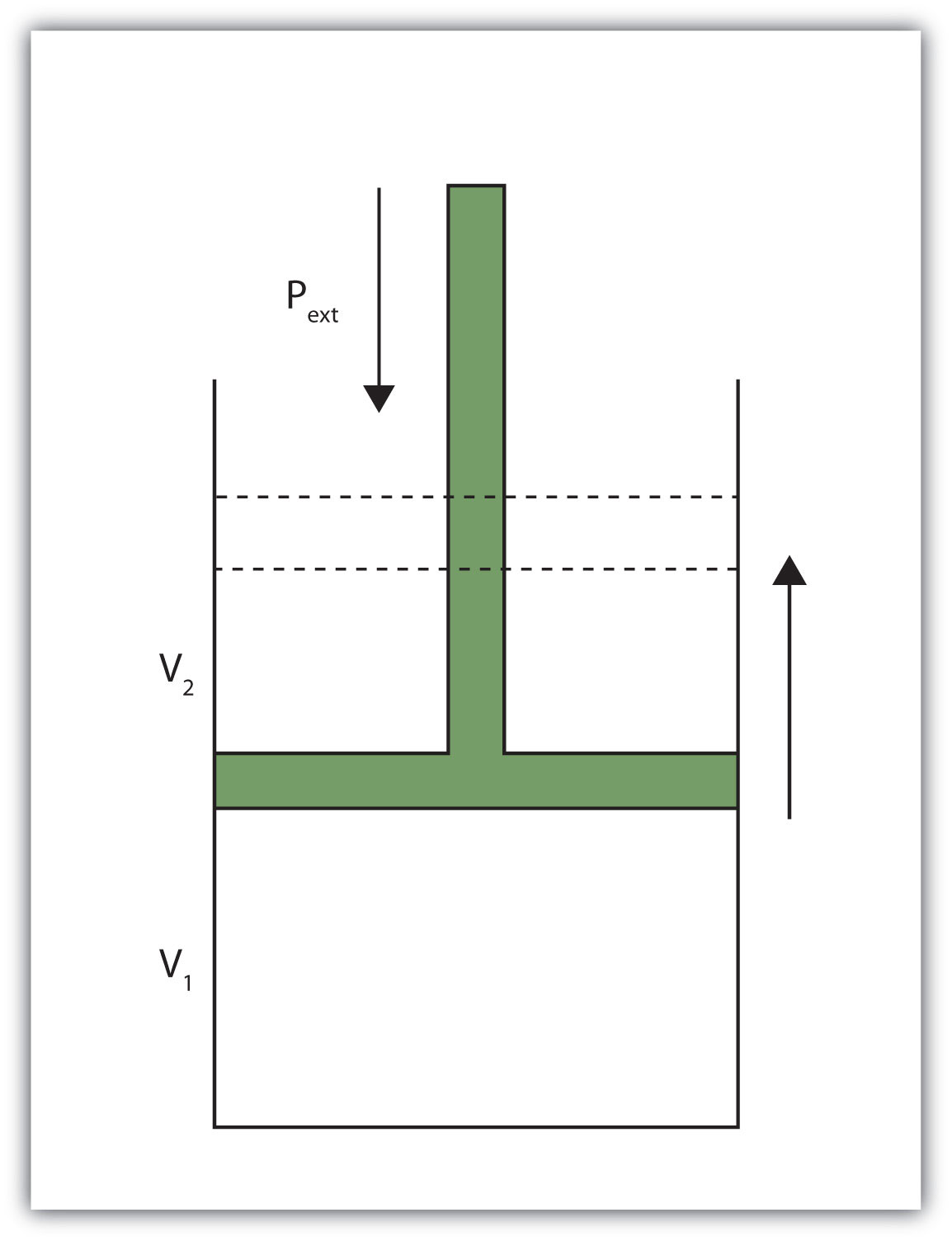
When a gas expands against an external pressure, the gas does work.
Finally, let us consider units. Volume changes are usually expressed in units like liters, while pressures are usually expressed in atmospheres. When we use the equation to determine work, the unit for work comes out as liter·atmospheres, or L·atm. This is not a very common unit for work. However, there is a conversion factor between L·atm and the common unit of work, joules:
1 L·atm = 101.32 J
Using this conversion factor and the previous equation for work, we can calculate the work performed when a gas expands or contracts.
Example 2 |
|
What is the work performed by a gas if it expands from 3.44 L to 6.19 L against a constant external pressure of 1.26 atm? Express the final answer in joules. Solution First we need to determine the change in volume, ΔV. A change is always the final value minus the initial value: ΔV = Vfinal − Vinitial = 6.19 L − 3.44 L = 2.75 L Now we can use the definition of work to determine the work done: w = −Pext · ΔV = −(1.26 atm)(2.75 L) = −3.47 L·atm Now we construct a conversion factor from the relationship between liter·atmospheres and joules:
We limit the final answer to three significant figures, as appropriate.
Test Yourself What is the work performed when a gas expands from 0.66 L to 1.33 L against an external pressure of 0.775 atm? Answer −53 J |
Heat is another aspect of energy. Heat is the transfer of energy from one body to another due to a difference in temperature. For example, when we touch something with our hands, we interpret that object as either hot or cold depending on how energy is transferred: If energy is transferred into your hands, the object feels hot. If energy is transferred from your hands to the object, your hands feel cold. Because heat is a measure of energy transfer, heat is also measured in joules.
For a given object, the amount of heat (q) involved is proportional to two things: the mass of the object (m) and the temperature change (ΔT) evoked by the energy transfer. We can write this mathematically as
where ∝ means “is proportional to.” To make a proportionality an equality, we include a proportionality constant. In this case, the proportionality constant is labeled c and is called the specific heat capacity, or, more succinctly, specific heat:
q = mcΔT
where the mass, specific heat, and change in temperature are multiplied together. Specific heat is a measure of how much energy is needed to change the temperature of a substance; the larger the specific heat, the more energy is needed to change the temperature. The units for specific heat are or , depending on what the unit of ΔT is. You may note a departure from the insistence that temperature be expressed in Kelvin. That is because a change in temperature has the same value whether the temperatures are expressed in degrees Celsius or kelvins.
Example 3 |
|
Calculate the heat involved when 25.0 g of Fe increase temperature from 22°C to 76°C. The specific heat of Fe is 0.449 J/g·°C. Solution First we need to determine ΔT. A change is always the final value minus the initial value: ΔT = 76°C − 22°C = 54°C
Now we can use the expression for q, substitute for all variables, and solve for heat:
Note how the g and °C units cancel, leaving J, a unit of heat. Also note that this value of q is inherently positive, meaning that energy is going into the system. Test Yourself Calculate the heat involved when 76.5 g of Ag increase temperature from 17.8°C to 144.5°C. The specific heat of Ag is 0.233 J/g·°C. Answer 2,260 J |
As with any equation, when you know all but one variable in the expression for q, you can determine the remaining variable by using algebra.
Example 4 |
|
It takes 5,408 J of heat to raise the temperature of 373 g of Hg by 104°C. What is the specific heat of Hg? Solution We can start with the equation for q, but now different values are given, and we need to solve for specific heat. Note that ΔT is given directly as 104°C. Substituting, 5,408 J = (373 g)c(104°C)
We divide both sides of the equation by 373 g and 104°C:
Combining the numbers and bringing together all the units, we get Test Yourself Gold has a specific heat of 0.129 J/g·°C. If 1,377 J are needed to increase the temperature of a sample of gold by 99.9°C, what is the mass of the gold? Answer 107 g |
Table 2.1 "Specific Heats of Various Substances" lists the specific heats of some substances. Specific heat is a physical property of substances, so it is a characteristic of the substance. The general idea is that the lower the specific heat, the less energy is required to change the temperature of the substance by a certain amount.
Table 2.1 Specific Heats of Various Substances
| Substance | Specific Heat (j/g.ºC) |
|---|---|
| water | 4.184 |
| iron | 0.449 |
| gold | 0.129 |
| mercury | 0.139 |
| aluminum | 0.900 |
| ethyl alcohol | 2.419 |
| magnesium | 1.03 |
| helium | 5.171 |
| oxygen | 0.918 |
Key Takeaways |
|
Exercises |
|
Learning Objectives |
|
Now that we have shown how energy, work, and heat are related, we are ready to consider energy changes in chemical reactions. A fundamental concept is that every chemical reaction occurs with a concurrent change in energy. Now we need to learn how to properly express these energy changes.
Our study of gases in Chapter 9 "Gases" and our definition of work in Section 2.2 "Work and Heat" indicate that conditions like pressure, volume, and temperature affect the energy content of a system. What we need is a definition of energy that holds when some of these conditions are specified (somewhat similar to our definition of standard temperature and pressure in our study of gases). We define the enthalpy change (ΔH) as the heat of a process when pressure is held constant:
The letter H stands for “enthalpy,” a kind of energy, while the Δ implies a change in the quantity. We will always be interested in the change in H, rather than the absolute value of H itself.
When a chemical reaction occurs, there is a characteristic change in enthalpy. The enthalpy change for a reaction is typically written after a balanced chemical equation and on the same line. For example, when two moles of hydrogen react with one mole of oxygen to make two moles of water, the characteristic enthalpy change is 570 kJ. We write the equation as
2H2(g) + O2(g) → 2H2O(ℓ) ΔH = −570 kJ
A chemical equation that includes an enthalpy change is called a thermochemical equation. A thermochemical equation is assumed to refer to the equation in molar quantities, which means it must be interpreted in terms of moles, not individual molecules.
Example 5 |
|
Write the thermochemical equation for the reaction of PCl3(g) with Cl2(g) to make PCl5(g), which has an enthalpy change of −88 kJ. Solution The thermochemical equation is PCl3(g) + Cl2(g) → PCl5(g) ΔH = −88 kJTest Yourself Write the thermochemical equation for the reaction of N2(g) with O2(g) to make 2NO(g), which has an enthalpy change of 181 kJ. Answer N2(g) + O2(g) → 2NO(g) ΔH = 181 kJ |
You may have noticed that the ΔH for a chemical reaction may be positive or negative. The number is assumed to be positive if it has no sign; a + sign can be added explicitly to avoid confusion. A chemical reaction that has a positive ΔH is said to be endothermic, while a chemical reaction that has a negative ΔH is said to be exothermic.
What does it mean if the ΔH of a process is positive? It means that the system in which the chemical reaction is occurring is gaining energy. If one considers the energy of a system as being represented as a height on a vertical energy plot, the enthalpy change that accompanies the reaction can be diagrammed as in part (a) in Figure 2.3 "Reaction Energy": the energy of the reactants has some energy, and the system increases its energy as it goes to products. The products are higher on the vertical scale than the reactants. Endothermic, then, implies that the system gains, or absorbs, energy.
An opposite situation exists for an exothermic process, as shown in part (b) in Figure 2.3 "Reaction Energy". If the enthalpy change of a reaction is negative, the system is losing energy, so the products have less energy than the reactants, and the products are lower on the vertical energy scale than the reactants are. Exothermic, then, implies that the system loses, or gives off, energy.
Figure 2.2 Reaction Energy
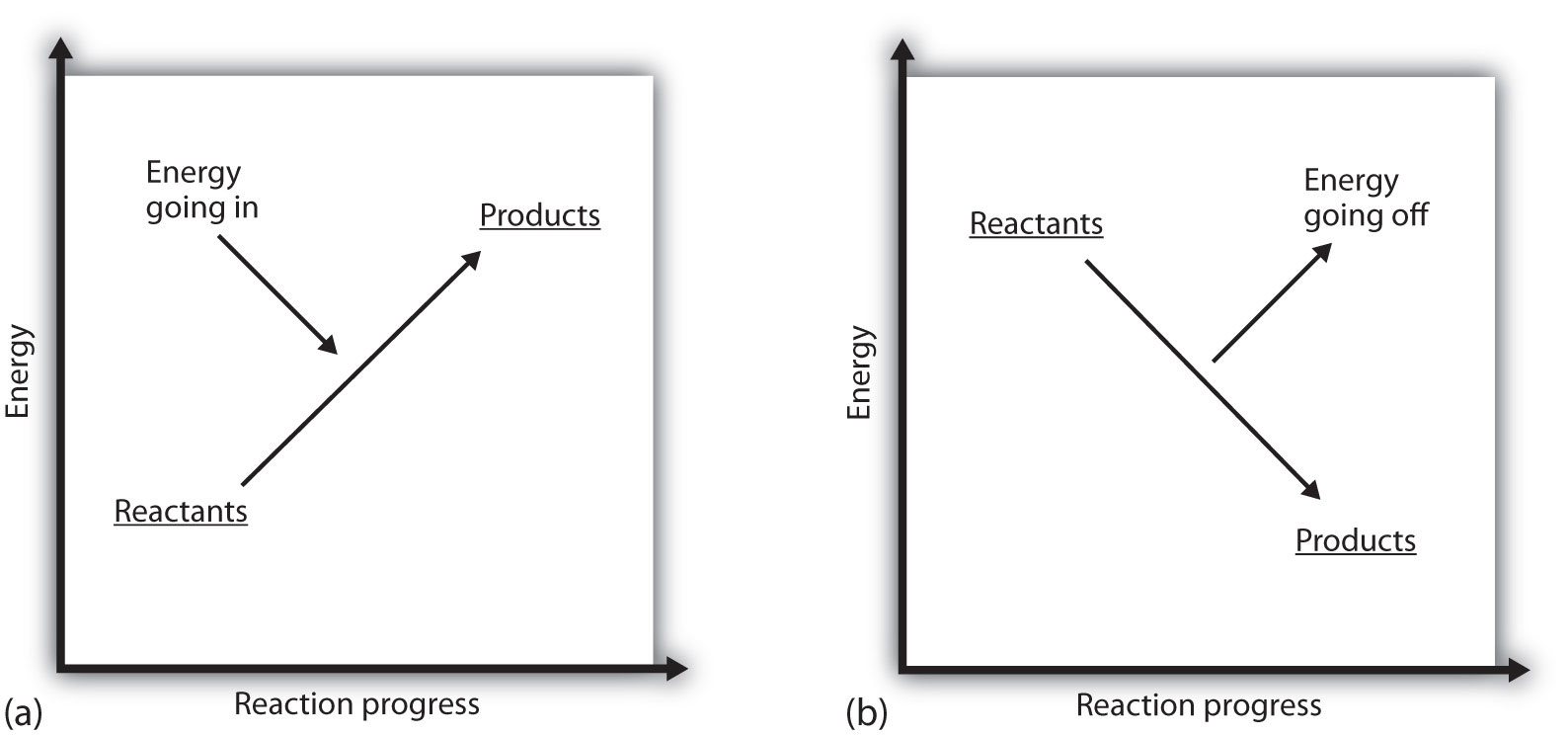
(a) In an endothermic reaction, the energy of the system increases (i.e., moves higher on the vertical scale of energy). (b) In an exothermic reaction, the energy of the system decreases (i.e., moves lower on the vertical scale of energy).
Example 6 |
|
Consider this thermochemical equation. 2CO(g) + O2(g) → 2CO2(g) ΔH = −565 kJ Is it exothermic or endothermic? How much energy is given off or absorbed? Solution By definition, a chemical reaction that has a negative ΔH is exothermic, meaning that this much energy—in this case, 565 kJ—is given off by the reaction. Test Yourself Consider this thermochemical equation. CO2(g) + H2(g) → CO(g) + H2O(g) ΔH = 42 kJ Is it exothermic or endothermic? How much energy is given off or absorbed? Answer Endothermic; 42 kJ are absorbed. |
How are ΔH values measured experimentally? Actually, ΔH is not measured; q is measured. But the measurements are performed under conditions of constant pressure, so ΔH is equal to the q measured.
Experimentally, q is measured by taking advantage of the equation
q = mcΔT
We premeasure the mass of the chemicals in a system. Then we let the chemical reaction occur and measure the change in temperature (ΔT) of the system. If we know the specific heat of the materials in the system (typically, we do), we can calculate q. That value of q is numerically equal to the ΔH of the process, which we can scale up to a molar scale. The container in which the system resides is typically insulated, so any energy change goes into changing the temperature of the system, rather than being leaked from the system. The container is referred to as a calorimeter, and the process of measuring changes in enthalpy is called calorimetry.
Figure 2.3 Calorimeters
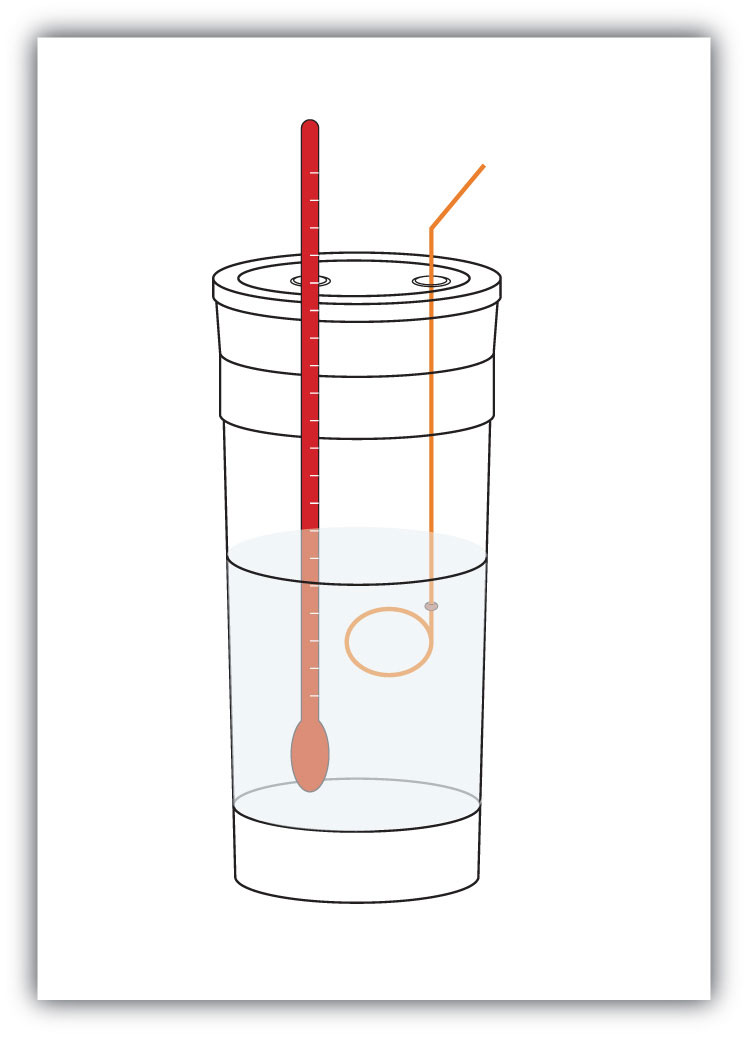
A simple calorimeter can be constructed from some nested foam coffee cups, a cover, a thermometer, and a stirrer.
For example, suppose 4.0 g of NaOH, or 0.10 mol of NaOH, are dissolved to make 100.0 mL of aqueous solution, while 3.65 g of HCl, or 0.10 mol of HCl, are dissolved to make another 100.0 mL of aqueous solution. The two solutions are mixed in an insulated calorimeter, a thermometer is inserted, and the calorimeter is covered (see Figure 2.4 "Calorimeters" for an example setup). The thermometer measures the temperature change as the following chemical reaction occurs:
NaOH (aq) + HCl(aq) → NaCl(aq) + H2O(ℓ)
An observer notes that the temperature increases from 22.4°C to 29.1°C. Assuming that the heat capacities and densities of the solutions are the same as those of pure water, we now have the information we need to determine the enthalpy change of the chemical reaction. The total amount of solution is 200.0 mL, and with a density of 1.00 g/mL, we thus have 200.0 g of solution. Using the equation for q, we substitute for our experimental measurements and the specific heat of water (Table 2.1 "Specific Heats of Various Substances"):
Solving for q, we get
The heat q is equal to the ΔH for the reaction because the chemical reaction occurs at constant pressure. However, the reaction is giving off this amount of energy, so the actual sign on ΔH is negative:
ΔH = −5,600 J for the reaction
Thus, we have the following thermochemical equation for the chemical reaction that occurred in the calorimeter:
The 1/10 coefficients are present to remind us that we started with one-tenth of a mole of each reactant, so we make one-tenth of a mole of each product. Typically, however, we report thermochemical equations in terms of moles, not one-tenth of a mole. To scale up to molar quantities, we must multiply the coefficients by 10. However, when we do this, we get 10 times as much energy. Thus, we have
NaOH (aq) + HCl(aq) → NaCl(aq) + H2O(ℓ) ΔH = −56,000 J
The ΔH can be converted into kJ units, so our final thermochemical equation is
NaOH (aq) + HCl(aq) → NaCl(aq) + H2O(ℓ) ΔH = −56 kJ
We have just taken our experimental data from calorimetry and determined the enthalpy change of a chemical reaction. Similar measurements on other chemical reactions can determine the ΔH values of any chemical reaction you want to study.
Example 7 |
|
A 100 mL solution of 0.25 mol of Ca2+(aq) was mixed with 0.50 mol of F−(aq) ions, and CaF2 was precipitated: Ca2+(aq) + 2F−(aq) → CaF2(s) The temperature of the solution increased by 10.5°C. What was the enthalpy change for the chemical reaction? What was the enthalpy change for the production of 1 mol of CaF2? Assume that the solution has the same density and specific heat as water. Solution Because we are given ΔT directly, we can determine the heat of the reaction, which is equal to ΔH: Solving for q, we get q = 4,400 J Therefore, ΔH = −4,400 J. According to the stoichiometry of the reaction, exactly 0.25 mol of CaF2 will form, so this quantity of heat is for 0.25 mol. For 1 mol of CaF2, we need to scale up the heat by a factor of four: q = 4,400 J × 4 = 17,600 J for 1 mol CaF2 On a molar basis, the change in enthalpy is ΔH = −17,600 J = −17.6 kJTest Yourself In a calorimeter at constant pressure, 0.10 mol of CH4(g) and 0.20 mol of O2(g) are reacted. CH4(g) + 2O2(g) → CO2(g) + 2H2O(ℓ) The reaction warms 750.0 g of H2O by 28.4°C. What is ΔH for the reaction on a molar scale? Answer −891 kJ |
Key Takeaways |
|
Exercises |
|
Learning Objective |
| Perform stoichiometry calculations using energy changes from thermochemical equations. |
We can relate quantities of one substance to another in a chemical equation by performing calculations that use the balanced chemical equation; the balanced chemical equation provides equivalences that we can use to construct conversion factors. For example, in the balanced chemical equation
2H2(g) + O2(g) → 2H2O(ℓ)
we recognized the equivalences
2 mol H2 ⇔ 1 mol O2 ⇔ 2 mol H2O
where ⇔ is the mathematical symbol for “is equivalent to.” In our thermochemical equation, however, we have another quantity—energy change:
2H2(g) + O2(g) → 2H2O(ℓ) ΔH = −570 kJ
This new quantity allows us to add another equivalence to our list:
2 mol H2 ⇔ 1 mol O2 ⇔ 2 mol H2O ⇔ −570 kJ
That is, we can now add an energy amount to the equivalences—the enthalpy change of a balanced chemical reaction. This equivalence can also be used to construct conversion factors so that we can relate enthalpy change to amounts of substances reacted or produced.
Note that these equivalences address a concern. When an amount of energy is listed for a balanced chemical reaction, what amount(s) of reactants or products does it refer to? The answer is that relates to the number of moles of the substance as indicated by its coefficient in the balanced chemical reaction. Thus, 2 mol of H2 are related to −570 kJ, while 1 mol of O2 is related to −570 kJ. This is why the unit on the energy change is kJ, not kJ/mol.
For example, consider the thermochemical equation
H2(g) + Cl2(g) → 2HCl(g) ΔH = −184.6 kJ
The equivalences for this thermochemical equation are
1 mol H2 ⇔ 1 mol Cl2 ⇔ 2 mol HCl ⇔ −184.6 kJ
Suppose we asked how much energy is given off when 8.22 mol of H2 react. We would construct a conversion factor between the number of moles of H2 and the energy given off, −184.6 kJ:
The negative sign means that this much energy is given off.
Example 8 |
|
Given the thermochemical equation N2(g) + 3H2(g) → 2NH3(g) ΔH = −91.8 kJhow much energy is given off when 222.4 g of N2 reacts? Solution The balanced thermochemical equation relates the energy change to moles, not grams, so we first convert the amount of N2 to moles and then use the thermochemical equation to determine the energy change: Test Yourself Given the thermochemical equation N2(g) + 3H2(g) → 2NH3(g) ΔH = −91.8 kJhow much heat is given off when 1.00 g of H2 reacts? Answer −15.1 kJ |
Like any stoichiometric quantity, we can start with energy and determine an amount, rather than the other way around.
Example 9 |
|
Given the thermochemical equation N2(g) + O2(g) → 2NO(g) ΔH = 180.6 kJif 558 kJ of energy are supplied, what mass of NO can be made? Solution This time, we start with an amount of energy: Test Yourself How many grams of N2 will react if 100.0 kJ of energy are supplied? N2(g) + O2(g) → 2NO(g) ΔH = 180.6 kJ
Answer 15.5 g |
Chemistry Is Everywhere: Welding with Chemical ReactionsOne very energetic reaction is called the thermite reaction. Its classic reactants are aluminum metal and iron(III) oxide; the reaction produces iron metal and aluminum oxide: 2Al(s) + Fe2O3(s) → Al2O3(s) + 2Fe(s) ΔH = −850.2 kJ When properly done, the reaction gives off so much energy that the iron product comes off as a liquid. (Iron normally melts at 1,536°C.) If carefully directed, the liquid iron can fill spaces between two or more metal parts and, after it quickly cools, can weld the metal parts together. Thermite reactions are used for this purpose even today. For civilian purposes, they are used to reweld broken locomotive axles that cannot be easily removed for repair. They are used to weld railroad tracks together. Thermite reactions can also be used to separate thin pieces of metal if, for whatever reason, a torch doesn’t work.
A small clay pot contains a thermite mixture. It is reacting at high temperature in the photo and will eventually produce molten metal to join the railroad tracks below it. Source: Photo courtesy of Skatebiker, http://commons.wikimedia.org/wiki/File:Velp-thermitewelding-1.jpg. Thermite reactions are also used for military purposes. Thermite mixtures are frequently used with additional components as incendiary devices—devices that start fires. Thermite reactions are also useful in disabling enemy weapons: a piece of artillery doesn’t work so well when it has a hole melted into its barrel because of a thermite reaction! |
Key Takeaway |
| The energy change of a chemical reaction can be used in stoichiometry calculations. |
Exercises |
|
Learning Objective |
| Learn how to combine chemical equations and their enthalpy changes. |
Now that we understand that chemical reactions occur with a simultaneous change in energy, we can apply the concept more broadly. To start, remember that some chemical reactions are rather difficult to perform. For example, consider the combustion of carbon to make carbon monoxide:
2C(s) + O2(g) → 2CO(g) ΔH = ?
In reality, this is extremely difficult to do; given the opportunity, carbon will react to make another compound, carbon dioxide:
2C(s) + O2(g) → 2CO2(g) ΔH = −393.5 kJ
Is there a way around this? Yes. It comes from the understanding that chemical equations can be treated like algebraic equations, with the arrow acting like the equals sign. Like algebraic equations, chemical equations can be combined, and if the same substance appears on both sides of the arrow, it can be canceled out (much like a spectator ion in ionic equations). For example, consider these two reactions:
2C(s) + 2O2(g) → 2CO2(g) 2CO2(g) → 2CO(g) + O2(g)
If we added these two equations by combining all the reactants together and all the products together, we would get
2C(s) + 2O2(g) + 2CO2(g) → 2CO2(g) + 2CO(g) + O2(g)
We note that 2CO2(g) appears on both sides of the arrow, so they cancel:
We also note that there are 2 mol of O2 on the reactant side, and 1 mol of O2 on the product side. We can cancel 1 mol of O2 from both sides:
What do we have left?
2C(s) + O2(g) → 2CO(g)
This is the reaction we are looking for! So by algebraically combining chemical equations, we can generate new chemical equations that may not be feasible to perform.
What about the enthalpy changes? Hess's law states that when chemical equations are combined algebraically, their enthalpies can be combined in exactly the same way. Two corollaries immediately present themselves:
What are the equations being combined? The first chemical equation is the combustion of C, which produces CO2:
2C(s) + 2O2(g) → 2CO2(g)
This reaction is two times the reaction to make CO2 from C(s) and O2(g), whose enthalpy change is known:
C(s) + O2(g) → CO2(g) ΔH = −393.5 kJ
According to the first corollary, the first reaction has an energy change of two times −393.5 kJ, or −787.0 kJ:
2C(s) + 2O2(g) → 2CO2(g) ΔH = −787.0 kJ
The second reaction in the combination is related to the combustion of CO(g):
2CO(g) + O2(g) → 2CO2(g) ΔH = −566.0 kJ
The second reaction in our combination is the reverse of the combustion of CO. When we reverse the reaction, we change the sign on the ΔH:
2CO2(g) → 2CO(g) + O2(g) ΔH = +566.0 kJ
Now that we have identified the enthalpy changes of the two component chemical equations, we can combine the ΔH values and add them:


Hess’s law is very powerful. It allows us to combine equations to generate new chemical reactions whose enthalpy changes can be calculated, rather than directly measured.
Example 10 |
|
Determine the enthalpy change of C2H4 + 3O2 → 2CO2 + 2H2O ΔH = ?
from these reactions: C2H2 + H2 → C2H4 ΔH = −174.5 kJ 2C2H2 + 5O2 → 4CO2 + 2H2O ΔH = −1,692.2 kJ 2CO2 + H2 → 2O2 + C2H2 ΔH = −167.5 kJ
Solution We will start by writing chemical reactions that put the correct number of moles of the correct substance on the proper side. For example, our desired reaction has C2H4 as a reactant, and only one reaction from our data has C2H4. However, it has C2H4 as a product. To make it a reactant, we need to reverse the reaction, changing the sign on the ΔH: C2H4 → C2H2 + H2 ΔH = +174.5 kJ
We need CO2 and H2O as products. The second reaction has them on the proper side, so let us include one of these reactions (with the hope that the coefficients will work out when all our reactions are added): 2C2H2 + 5O2 → 4CO2 + 2H2O ΔH = −1,692.2 kJ
We note that we now have 4 mol of CO2 as products; we need to get rid of 2 mol of CO2. The last reaction has 2CO2 as a reactant. Let us use it as written: 2CO2 + H2 → 2O2 + C2H2 ΔH = −167.5 kJ
We combine these three reactions, modified as stated: C2H4 + 3O2 → 2CO2 + 2H2O ΔH = ?
What cancels? 2C2H2, H2, 2O2, and 2CO2. What is left is C2H4 + 3O2 → 2CO2 + 2H2Owhich is the reaction we are looking for. The ΔH of this reaction is the sum of the three ΔH values: ΔH = +174.5 − 1,692.2 − 167.5 = −1,685.2 kJ
Test Yourself Given the thermochemical equations Pb + Cl2 → PbCl2 ΔH = −223 kJ PbCl2 + Cl2 → PbCl4 ΔH = −87 kJdetermine ΔH for 2PbCl2 → Pb + PbCl4
Answer +136 kJ |
Key Takeaway |
| Hess’s law allows us to combine reactions algebraically and then combine their enthalpy changes the same way. |
Exercises |
|
Learning Objectives |
|
Hess’s law allows us to construct new chemical reactions and predict what their enthalpies of reaction will be. This is a very useful tool because now we don’t have to measure the enthalpy changes of every possible reaction. We need measure only the enthalpy changes of certain benchmark reactions and then use these reactions to algebraically construct any possible reaction and combine the enthalpies of the benchmark reactions accordingly.
But what are the benchmark reactions? We need to have some agreed-on sets of reactions that provide the central data for any thermochemical equation.
Formation reactions are chemical reactions that form one mole of a substance from its constituent elements in their standard states. By standard states we mean as a diatomic molecule if that is how the element exists and the proper phase at normal temperatures (typically room temperature). The product is one mole of substance, which may require that coefficients on the reactant side be fractional (a change from our normal insistence that all coefficients be whole numbers). For example, the formation reaction for methane (CH4) is
C(s) + 2H2(g) → CH4(g)
The formation reaction for carbon dioxide (CO2) is
C(s) + O2(g) → CO2(g)
In both cases, one of the elements is a diatomic molecule because that is the standard state for that particular element. The formation reaction for H2O—
2H2(g) + O2(g) → 2H2O(ℓ)
—is not in a standard state because the coefficient on the product is 2; for a proper formation reaction, only one mole of product is formed. Thus, we have to divide all coefficients by 2:
H2(g) + 1/2O2(g) → H2O(ℓ)
On a molecular scale, we are using half of an oxygen molecule, which may be problematic to visualize. However, on a molar level, it implies that we are reacting only half of a mole of oxygen molecules, which should be an easy concept for us to understand.
Example 11 |
|
Which of the following are proper formation reactions?
Solution
Test Yourself Is this a proper formation reaction? Explain why or why not. 2Fe(s) + 3P(s) + 12O(g) → Fe2(PO4)3(s)Answer This is not a proper formation reaction because oxygen is not written as a diatomic molecule. |
Given the formula of any substance, you should be able to write the proper formation reaction for that substance.
Example 12 |
|
Write formation reactions for each of the following.
Solution In both cases, there is one mole of the substance as product, and the coefficients of the reactants may have to be fractional to balance the reaction.
Test Yourself Write the equation for the formation of CaCO3(s). Answer Ca(s) + C(s) + 3/2O2(g) → CaCO3(s) |
The enthalpy change for a formation reaction is called the enthalpy of formation and is given the symbol ΔHf. The subscript f is the clue that the reaction of interest is a formation reaction. Thus, for the formation of FeO(s),
Note that now we are using kJ/mol as the unit because it is understood that the enthalpy change is for one mole of substance. Note, too, by definition, that the enthalpy of formation of an element is exactly zero because making an element from an element is no change. For example,
H2(g) → H2(g) ΔHf = 0
Formation reactions and their enthalpies are important because these are the thermochemical data that are tabulated for any chemical reaction. Table 7.2 "Enthalpies of Formation for Various Substances" lists some enthalpies of formation for a variety of substances; in some cases, however, phases can be important (e.g., for H2O).
It is easy to show that any general chemical equation can be written in terms of the formation reactions of its reactants and products, some of them reversed (which means the sign must change in accordance with Hess’s law). For example, consider
2NO2(g) → N2O4(g)
We can write it in terms of the (reverse) formation reaction of NO2 and the formation reaction of N2O4:



We must multiply the first reaction by 2 to get the correct overall balanced equation. We are simply using Hess’s law in combining the ΔHf values of the formation reactions.
Table 2.2 Enthalpies of Formation for Various Substances
Compound |
ΔHf (kJ/mol) | Compound | ΔHf (kJ/mol) | Compound | ΔHf (kJ/mol) | Compound | ΔHf (kJ/mol) |
|---|---|---|---|---|---|---|---|
| Ag(s) | 0 | Ca(s) | 0 | Hg2Cl2(s) | −265.37 | NaHCO3(s) | −950.81 |
| AgBr(s) | −100.37 | CaCl2(s) | −795.80 | I2(s) | 0 | NaN3(s) | 21.71 |
| AgCl(s) | −127.01 | CaCO3(s, arag) | −1,207.1 | K(s) | 0 | Na2CO3(s) | −1,130.77 |
| Al(s) | 0 | CaCO3(s, calc) | −1,206.9 | KBr(s) | −393.8 | Na2O(s) | −417.98 |
| Al2O3(s) | −1,675.7 | Cl2(g) | 0 | KCl(s) | −436.5 | Na2SO4(s) | −331.64 |
| Ar(g) | 0 | Cr(s) | 0 | KF(s) | −567.3 | Ne(g) | 0 |
| Au(s) | 0 | Cr2O3(s) | −1,134.70 | KI(s) | −327.9 | Ni(s) | 0 |
| BaSO4(s) | −1,473.19 | Cs(s) | 0 | Li(s) | 0 | O2(g) | 0 |
| Br2(ℓ) | 0 | Cu(s) | 0 | LiBr(s) | −351.2 | O3(g) | 142.67 |
| C(s, dia) | 1.897 | F2(g) | 0 | LiCl(s) | −408.27 | PH3(g) | 22.89 |
| C(s, gra) | 0 | Fe(s) | 0 | LiF(s) | −616.0 | Pb(s) | 0 |
| CCl4(ℓ) | −128.4 | Fe2(SO4)3(s) | −2,583.00 | LiI(s) | −270.4 | PbCl2(s) | −359.41 |
| CH2O(g) | −115.90 | Fe2O3(s) | −825.5 | Mg(s) | 0 | PbO2(s) | −274.47 |
| CH3COOH(ℓ) | −483.52 | Ga(s) | 0 | MgO(s) | −601.60 | PbSO4(s) | −919.97 |
| CH3OH(ℓ) | −238.4 | HBr(g) | −36.29 | NH3(g) | −45.94 | Pt(s) | 0 |
| CH4(g) | −74.87 | HCl(g) | −92.31 | NO(g) | 90.29 | S(s) | 0 |
| CO(g) | −110.5 | HF(g) | −273.30 | NO2(g) | 33.10 | SO2(g) | −296.81 |
| CO2(g) | −393.51 | HI(g) | 26.5 | N2(g) | 0 | SO3(g) | −395.77 |
| C2H5OH(ℓ) | −277.0 | HNO2(g) | −76.73 | N2O(g) | 82.05 | SO3(ℓ) | −438 |
| C2H6(g) | −83.8 | HNO3(g) | −134.31 | N2O4(g) | 9.08 | Si(s) | 0 |
| C6H12(ℓ) | −157.7 | H2(g) | 0 | N2O5(g) | 11.30 | U(s) | 0 |
| C6H12O6(s) | −1277 | H2O(g) | −241.8 | Na(s) | 0 | UF6(s) | −2,197.0 |
| C6H14(ℓ) | −198.7 | H2O(ℓ) | −285.83 | NaBr(s) | −361.1 | UO2(s) | −1,085.0 |
| C6H5CH3(ℓ) | 12.0 | H2O(s) | −292.72 | NaCl(s) | −385.9 | Xe(g) | 0 |
| C6H6(ℓ) | 48.95 | He(g) | 0 | NaF(s) | −576.6 | Zn(s) | 0 |
| C10H8(s) | 77.0 | Hg(ℓ) | 0 | NaI(s) | −287.8 | ZnCl2(s) | −415.05 |
| C12H22O11(s) | −2,221.2 |
Sources: National Institute of Standards and Technology’s Chemistry WebBook, http://webbook.nist.gov/chemistry; D. R. Lide, ed., CRC Handbook of Chemistry and Physics, 89th ed. (Boca Raton, FL: CRC Press, 2008); J. A. Dean, ed., Lange’s Handbook of Chemistry, 14th ed. (New York: McGraw-Hill, 1992).
Example 13 |
|
Show that the reaction Fe2O3(s) + 3SO3(g) → Fe2(SO4)3(s) can be written as a combination of formation reactions. Solution There will be three formation reactions. The one for the products will be written as a formation reaction, while the ones for the reactants will be written in reverse. Furthermore, the formation reaction for SO3 will be multiplied by 3 because there are three moles of SO3 in the balanced chemical equation. The formation reactions are as follows: 2Fe(s) + 3S(s) + 6O2(g) → Fe2(SO4)3(s)
When these three equations are combined and simplified, the overall reaction is Fe2O3(s) + 3SO3(s) → Fe2(SO4)3(s)Test Yourself Write the formation reactions that will yield 2SO2(g) + O2(g) → 2SO3(g).Answer |
Now that we have established formation reactions as the major type of thermochemical reaction we will be interested in, do we always need to write all the formation reactions when we want to determine the enthalpy change of any random chemical reaction? No. There is an easier way. You may have noticed in all our examples that we change the signs on all the enthalpies of formation of the reactants, and we don’t change the signs on the enthalpies of formation of the products. We also multiply the enthalpies of formation of any substance by its coefficient—technically, even when it is just 1. This allows us to make the following statement: the enthalpy change of any chemical reaction is equal to the sum of the enthalpies of formation of the products minus the sum of the enthalpies of formation of the reactants. In mathematical terms,
where np and nr are the number of moles of products and reactants, respectively (even if they are just 1 mol), and ΔHf,p and ΔHf,r are the enthalpies of formation of the product and reactant species, respectively. This products-minus-reactants scheme is very useful in determining the enthalpy change of any chemical reaction, if the enthalpy of formation data are available. Because the mol units cancel when multiplying the amount by the enthalpy of formation, the enthalpy change of the chemical reaction has units of energy (joules or kilojoules) only.
Example 14 |
|
Use the products-minus-reactants approach to determine the enthalpy of reaction for Solution The enthalpies of formation are multiplied by the number of moles of each substance in the chemical equation, and the total enthalpy of formation for reactants is subtracted from the total enthalpy of formation of the products:
All the mol units cancel. Multiplying and combining all the values, we get ΔHrxn = −112.0 kJ Test Yourself What is the enthalpy of reaction for this chemical equation? Answer +2.8 kJ |
Food and Drink App: Calories and NutritionThe "Energy" section mentioned the connection between the calorie unit and nutrition: the calorie is the common unit of energy used in nutrition, but we really consider the kilocalorie (spelled Calorie with a capital C). A daily diet of 2,000 Cal is actually 2,000,000 cal, or over 8,000,000 J, of energy. Nutritionists typically generalize the Calorie content of foods by separating it into the three main food types: proteins, carbohydrates, and fats. The general rule of thumb is as follows:
This table is very useful. Assuming a 2,000 Cal daily diet, if our diet consists solely of proteins and carbohydrates, we need only about 500 g of food for sustenance—a little more than a pound. If our diet consists solely of fats, we need only about 220 g of food—less than a half pound. Of course, most of us have a mixture of proteins, carbohydrates, and fats in our diets. Water has no caloric value in the diet, so any water in the diet is calorically useless. (However, it is important for hydration; also, many forms of water in our diet are highly flavored and sweetened, which bring other nutritional issues to bear.) When your body works, it uses calories provided by the diet as its energy source. If we eat more calories than our body uses, we gain weight—about 1 lb of weight for every additional 3,500 Cal we ingest. Similarly, if we want to lose weight, we need to expend an extra 3,500 Cal than we ingest to lose 1 lb of weight. No fancy or fad diets are needed; maintaining an ideal body weight is a straightforward matter of thermochemistry—pure and simple. |
Key Takeaways |
|
Exercises |
|
Additional Exercises |
|
Library Info and Research Help | reflibrarian@hostos.cuny.edu (718) 518-4215
Loans or Fines | circ@hostos.cuny.edu (718) 518-4222
475 Grand Concourse (A Building), Room 308, Bronx, NY 10451
